Next: Max-flow Problem Up: advalect2 Previous: advalect2
One often uses graphs to model transportation networks - networks whose edges carry some sort of traffic and whose nodes act as “switches” passing traffic between different edges. The flow may be of oil or water in pipelines, electricity, or phone calls, emails in networks, or traffic in networks. Consider an example of high-way system in which the edges are highways and the nodes are interchanges; or a computer network in which the edges are the links that carry packets and the nodes are switches, or a fluid network in which edges are pipes and that carry liquid, and the nodes are junctures where pipes plugged together. The network models of this category have several ingredients: capacities on edges, including how much they can carry; source nodes in the graph, which generate traffic; and the traffic itself which is transmitted across the edges.
Networks are important for both electronic communication and for transport of goods. The problem of efficiently moving entities (such as bits, people, or products) from one place to other in an underlying network is modeled by network flow. The problem plays central role in the fields of operations research and computer science, and much emphasis has been placed on the design of efficient algorithms for solving it. Many of the basic algorithms plays important role in understanding the network flow algorithms.
The matching, we studied earlier, is a special case of flow problem - match the flow with capacity of edge so that over all flow is maximum. Assignment is a generalization of the matching problem to the wighted case.
Flow network. A flow network





Before we proceed further, we shall make some assumptions: 1) no edge enters the source 

![[*]](crossref.png) shows an example of such network, with capacity
shows an example of such network, with capacity 
Flow. An s-t is a function



A flow function is required to satisfy the following constraints:
 ,
,
 ,
,
 , there is
, there is

 , we require
, we require
 |
(2.1) |
Whenever,




The capacity constraint says that the total flow on an edge does not exceed its capacity. The skew symmetry condition says that the flow on an edge is the negative of the flow in the reverse direction. The flow conservation constraint says that the total net flow out of any vertex other than the source and sink is zero. The value of this of net flow flow from 
In the maximum-flow problem the objective is to find a flow function that satisfies these three constraints, and also maximizes the total flow value 

The above formulation of the network flow problem is powerful enough to capture generalization where there are many sources and sinks (single commodity flow), and where both vertices and edges have capacity constraints.
We call the non-negative quantity 



that is, total flow out of a source minus the flow into the source. Typically, the value




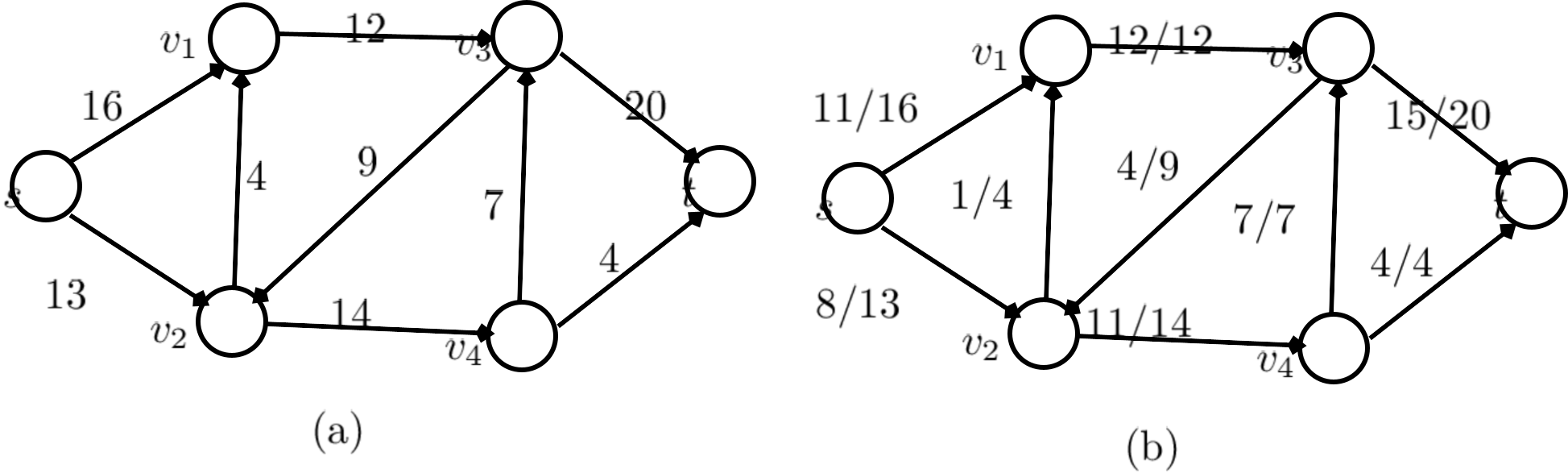
![[*]](crossref.png) , where Figure
, where Figure ![[*]](crossref.png) (a) shows the capacities
(a) shows the capacities  of all edges, and figure
of all edges, and figure ![[*]](crossref.png) (b) shows flows/capacities, i.e.,
(b) shows flows/capacities, i.e.,
 of all edges.
of all edges.
|